The stresses at the integration points are the most accurate. Korg Triton Le Boje Download Free. They occur inside the element and may not be the highest stress in the area; for example around a fillet radius the free surface stress will be higher than the integration point stress. The element shape function is used to extrapolate the integration point stresses out to the element nodes - these are in a useful location like a fillet radius free surface or a hole edge. Adjacent elements combined with their shape functions will predict different stress values at their common nodes. The question then arises which stress do you believe? Rev From Dvl Love Arigatou Mp3 Download. Most FE packages average the stresses for each element at the node.

If the unaveraged stresses are within a few percent of each other I go ahead and use averaged nodal stresses. If the unaveraged stresses are significantly different, I use peak unaveraged stresses, or refine the mesh to get a better result. Multicharts 8 7 Cracker.

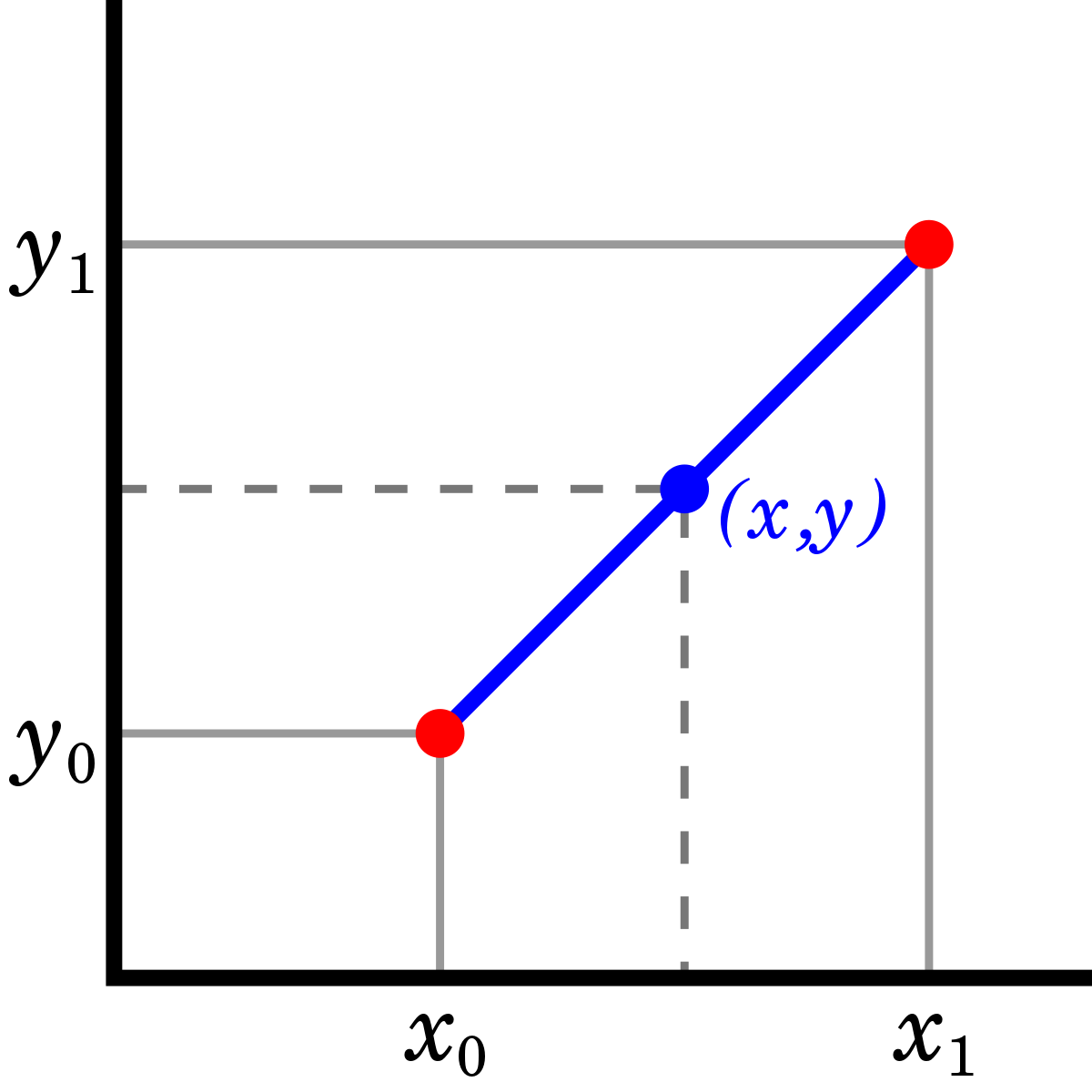
Program this into your calculator. • x - independent variable entries (vector). • y - dependent variable entries (vector). • xi - value(s) where. Polynomial Interpolation. Given n+1 data points, we can fit an nth-degree polynomial. Two steps: 1. Obtain polynomial coefficients by solving the set of linear. Free Statistical Software This page contains links to free software packages that you can download and install on your computer for stand-alone (offline, non-Internet.

IN ALL CASES, UNAVERAGED NODAL STRESSES MUST BE CHECKED BEFORE USING AVERAGED NODAL STRESSES. WHEN USING SHELL, BEAM, OR ANY OTHER ELEMENT FOR WHICH RESULTS ARE PRESENTED IN SOME FORM OF LOCAL SYSTEM, AVERAGED NODAL STRESSES SHOULD NOT BE USED UNLESS YOU REALLY KNOW WHAT YOU ARE DOING. I can't count the number of expensive fatigue errors which I have seen as a consequence of averaged nodal stresses. Amen RE: Stress at integration points or at nodes? (Structural) 4 Dec 08 10:02.

Gwolf2 and others: I have often heard the statement in this forum that 'stresses at integration points are most accurate.' Can anybody provide proof (say a refereed journal article, a section of a book, or a study you have made which has enough details to repeat the study ourselves) of that assertion? It seems intuitive that this statement is true in a nonlinear analysis because you use the stresses at the integration points in the nonlinear iteration (say a Newton Raphson iteration is used to solve the nonlinear equations). However, the 'truth' of this 'stresses are most accurate at the integration points' statement doesn't seem so obvious in a linear analysis, since all you are doing is solving Ku=f, and there is no need to calculate the stresses at the integration points until you perform the post processing.

RE: Stress at integration points or at nodes? (Aerospace) 4 Dec 08 10:26. Depends on what you mean by accurate, I'd interject. If 'accuracy' means 'correct for the linearized, discretized system of equations that was created to approximate a solid body deforming under load', then, yes, the stresses are correct only at the integration points, and are extrapolated to the edges of each element.